1.
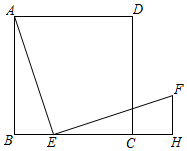
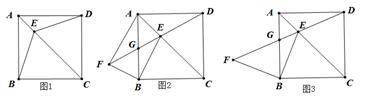
如图, 正方形  中,
中,  4 , 动点
4 , 动点  从点
从点  出发沿
出发沿  向点
向点  运动,连结
运动,连结  , 以
, 以  为边在其右侧作正方形
为边在其右侧作正方形  与
与  相交于点
相交于点  .
.

(1)
在点  的运动过程中, 点
的运动过程中, 点  的位置也随之改变, 则点
的位置也随之改变, 则点  始终在直线
始终在直线  上吗? 如果在, 请给出证明, 如果不在, 请说明理由.
(2)
当点
上吗? 如果在, 请给出证明, 如果不在, 请说明理由.
(2)
当点  在
在  边上运动时,
边上运动时,  的面积如何变化? 请写出推理过程.
的面积如何变化? 请写出推理过程.
【考点】
勾股定理;
正方形的性质;
三角形全等的判定-SAS;