1.
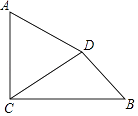
如图,在  中,
中,  ,
,  ,点P在线段
,点P在线段  ,作射线
,作射线 
 ,将射线
,将射线  绕点C逆时针旋转
绕点C逆时针旋转  ,得到射线
,得到射线  ,过点A作
,过点A作  于点D,交
于点D,交  于点E,连接
于点E,连接  .
.
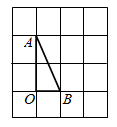
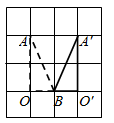
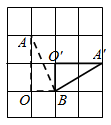
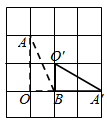
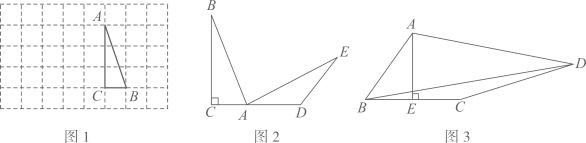
(1)
依题意补全图形;
(2)
用等式表示线段  ,
,  ,
,  之间的数量关系,并证明.
之间的数量关系,并证明.
【考点】
旋转的性质;
作图﹣旋转;
能力提升
真题演练