已知抛物线的对称轴为直线x=2，且经过点A（0，3）和点B（3，0）.

0 返回出卷网首页

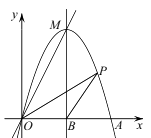
1. 已知抛物线的对称轴为直线x=2，且经过点A（0，3）和点B（3，0）.

(1) 求抛物线的解析式；

(2) 点C坐标为（2，－ $\text{[math]}$ ），过点D(0，－ $\text{[math]}$ ）作x轴的平行线l，设抛物线上的任意一点P到直线l 的距离为d，求证：PC=d；

(3) 点E在y轴上(点E位于点A下方），点M，N在抛物线上(点M，N均不同于点A，点M在点N左侧)，直线EM，EN与抛物线均有唯一公共点，直线MN交y轴于点F，求证：点A为线段EF的中点.

【考点】

待定系数法求二次函数解析式; 二次函数与一次函数的综合应用; 二次函数图象上点的坐标特征;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在平面直角坐标系中，点O为坐标原点，直线y=kx+1（k≠0）与x轴交于点A，与y轴交于点C，过点C的抛物线y=ax²﹣（6a﹣2）x+b（a≠0）与直线AC交于另一点B，点B坐标为（4，3）．

(1) 求a的值.

(2) 点P是射线CB上的一个动点，过点P作PQ⊥x轴，垂足为点Q，在x轴上点Q的右侧取点M，使MQ= $\text{[math]}$ ，在QP的延长线上取点N，连接PM，AN，已知tan∠NAQ-tan∠MPQ= $\text{[math]}$ ，求线段PN的长；

(3) 在（2）的条件下，过点C作CD⊥AB，使点D在直线AB下方，且CD=AC，连接PD，NC，当以PN，PD，NC的长为三边长构成的三角形面积是 $\text{[math]}$ 时，在y轴左侧的抛物线上是否存在点E，连接NE，PE，使得△ENP与以PN，PD，NC的长为三边长的三角形全等？若存在，求出E点坐标；若不存在，请说明理由．

综合题困难

2. 如图，抛物线 $\text{[math]}$ 交 $\text{[math]}$ 轴正半轴于点A，直线 $\text{[math]}$ 经过抛物线的顶点M．已知该抛物线的对称轴为直线 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点B．

(1) 求a，b的值．

(2) P是第一象限内抛物线上的一点，且在对称轴的右侧，连接OP，BP．设点P的横坐标为 $\text{[math]}$ ，△OBP的面积为S，记 $\text{[math]}$ ．求K关于 $\text{[math]}$ 的函数表达式及K的范围．

综合题普通

3. 已知抛物线 $\text{[math]}$ 交 $\text{[math]}$ 轴于 $\text{[math]}$ 两点， $\text{[math]}$ 为抛物线的顶点， $\text{[math]}$ 为抛物线上不与 $\text{[math]}$ 重合的相异两点，记 $\text{[math]}$ 中点为 $\text{[math]}$ ，直线 $\text{[math]}$ 的交点为 $\text{[math]}$ ．

(1) 求抛物线的函数表达式；

(2) 若 $\text{[math]}$ ，且 $\text{[math]}$ ，求证： $\text{[math]}$ 三点共线；

(3) 小明研究发现：无论 $\text{[math]}$ 在抛物线上如何运动，只要 $\text{[math]}$ 三点共线， $\text{[math]}$ 中必存在面积为定值的三角形．请直接写出其中面积为定值的三角形及其面积，不必说明理由．

综合题困难