某农场要建一个饲养场（矩形ABCD），两面靠墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图所示的三处各留1米宽的门（不用木栏）.建成后木栏总长45米.

0 返回出卷网首页

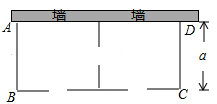
1. 某农场要建一个饲养场（矩形ABCD），两面靠墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图所示的三处各留1米宽的门（不用木栏）.建成后木栏总长45米.

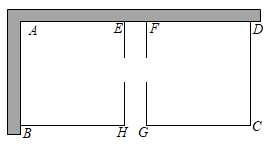
(1) 若饲养场（矩形ABCD）的一边CD长为8米，则另一边BC＝米.

(2) 若饲养场（矩形ABCD）的面积为180平方米，求边CD的长.

(3) 饲养场的面积能达到210平方米吗？若能达到，求出边CD的长；若不能达到，请说明理由.

【考点】

一元二次方程的应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 某农场要建一个饲养场（长方形ABCD），饲养场的一面靠墙（墙最大可用长度为27米），另三边用木栏围成，中间也用木栏隔开，分成两个场地，并在如图所示的三处各留1米宽的门（不用木栏），建成后木栏总长57米，设饲养场（长方形ABCD）的宽为a米

(1) 饲养场的长为米（用含a的代数式表示）

(2) 若饲养场的面积为288 $\text{[math]}$ ，求a的值

综合题普通

2. 如图1，有一张长 $\text{[math]}$ 宽 $\text{[math]}$ 的长方形硬纸片，裁去角上 $\text{[math]}$ 个小正方形和 $\text{[math]}$ 个小长方形（图中阴影部分）之后，恰好折成如图2的有盖纸盒.

(1) 若纸盒的高是 $\text{[math]}$ cm，求纸盒底面长方形的长和宽；

(2) 若纸盒的底面积是 $\text{[math]}$ ，求纸盒的高.

综合题普通

3. 实验基地有一长为 10 米的墙 $\text{[math]}$ ，研究小组想利用墙 $\text{[math]}$ 和长 37 米的篱笆，在前面的空地围出一个矩形种植园，且在墙对面的篱笆上开一个宽为 1 米的门。

(1) 小徐按图 1 的方案围成矩形种植园（边 $\text{[math]}$ 为墙 $\text{[math]}$ 的一部分），当矩形种植园的面积为 $\text{[math]}$ 时，求出矩形种植园一边 $\text{[math]}$ 的长。

(2) 小祝按照图 2 的方案围成矩形种植园 (墙 $\text{[math]}$ 为边 $\text{[math]}$ 的一部分)，能否围成面积为 $\text{[math]}$ 的矩形种植园，若能，请求出矩形种植园的一组邻边长；若不能，请说明理由。

综合题普通