1.
在等腰  中,
中,  ,点D是
,点D是  边上一点(不与点B、C重合),连结
边上一点(不与点B、C重合),连结  .
.

(1)
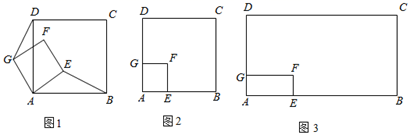
如图1,若  ,点D关于直线
,点D关于直线  的对称点为点E,结
的对称点为点E,结  ,
,  ,则
,则  ;
(2)
若
;
(2)
若  ,将线段
,将线段  绕点A顺时针旋转
绕点A顺时针旋转  得到线段
得到线段  ,连结
,连结  .
(3)
如图3,若
.
(3)
如图3,若  ,且
,且  ,试探究
,试探究  、
、  、
、  之间满足的数量关系,并证明.
之间满足的数量关系,并证明.
①在图2中补全图形;
②探究 与
的数量关系,并证明;
【考点】
等边三角形的判定与性质;
相似三角形的判定与性质;
旋转的性质;
三角形全等的判定-SAS;
能力提升