如图

0 返回出卷网首页

1. 如图

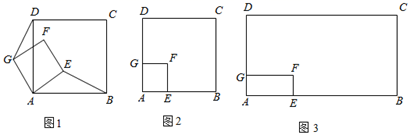
(1) 问题探究：如图1所示，有公共顶点A的两个正方形ABCD和正方形AEFG.AE＜AB，连接BE与DG，请判断线段BE与线段DG之间有怎样的数量关系和位置关系.并请说明理由.

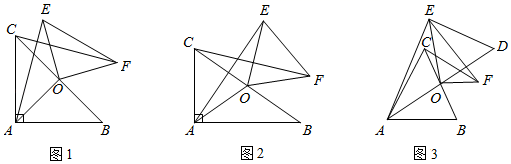
(2) 理解应用：如图2所示，有公共顶点A的两个正方形ABCD和正方形AEFG，AE＜AB，AB＝10，将正方形AEFG绕点A在平面内任意旋转，当∠ABE＝15°，且点D、E、G三点在同一条直线上时，请直接写出AE的长；

(3) 拓展应用：如图3所示，有公共顶点A的两个矩形ABCD和矩形AEFG，AD＝4 $\text{[math]}$ ，AB＝4 $\text{[math]}$ ，AG＝4，AE＝4 $\text{[math]}$ ，将矩形AEFG绕点A在平面内任意旋转，连接BD，DE，点M，N分别是BD，DE的中点，连接MN，当点D、E、G三点在同一条直线上时，请直接写出MN的长

【考点】

相似三角形的判定与性质; 旋转的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知 $\text{[math]}$ 和 $\text{[math]}$ 有公共的顶点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ． $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 若点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在一条直线上，如图1，求证： $\text{[math]}$ ；

(2) 将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针方向旋转一定的角度， $\text{[math]}$ 的延长线交 $\text{[math]}$ 于点 $\text{[math]}$ ，如图2

①证明： $\text{[math]}$ ；

②若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

综合题普通

2. 某学习小组开展了图形旋转的探究活动：将一个矩形 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ ，得到矩形 $\text{[math]}$ ，连结 $\text{[math]}$ ．

(1) 如图1，当 $\text{[math]}$ 时，点 $\text{[math]}$ 恰好在 $\text{[math]}$ 延长线上．若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

(2) 如图2，连结 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点M．观察思考线段 $\text{[math]}$ 与 $\text{[math]}$ 数量关系并说明理由．

(3) 在（2）的条件下，射线 $\text{[math]}$ 交 $\text{[math]}$ 于点N（如图3），若 $\text{[math]}$ ，旋转角 $\text{[math]}$ 等于多少度时 $\text{[math]}$ 是等边三角形，请写出 $\text{[math]}$ 的值，并说明 $\text{[math]}$ 是等边三角形的理由．

综合题困难

3. 如图，在Rt△ABC中， $\text{[math]}$ ， AC＝BC，D为斜边AB上一动点（不与端点A，B重合），以C为旋转中心，将CD逆时针旋转90°得到CE，连接AE，BE，F为AE的中点．

(1) 求证： $\text{[math]}$ ；

(2) 用等式表示线段CD，BE，CF三者之间数量关系，并说明理由；

(3) 若CF＝ $\text{[math]}$ ， CD＝ $\text{[math]}$ ，求 $\text{[math]}$ 的值．

综合题困难