综合与实践．特例感知．两块三角板△ADB与△EFC全等，∠ADB＝∠EFC＝90°，∠B＝45°，AB＝6．

0 返回出卷网首页

1. 综合与实践．特例感知．两块三角板△ADB与△EFC全等，∠ADB＝∠EFC＝90°，∠B＝45°，AB＝6．

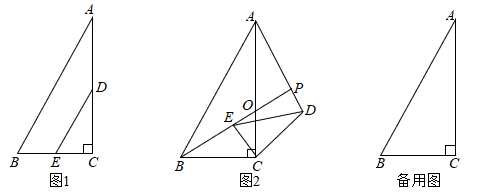
(1) 将直角边AD和EF重合摆放．点P、Q分别为BE、AF的中点，连接PQ，如图1．则△APQ的形状为．

(2) 操作探究

若将△EFC绕点C顺时针旋转45°，点P恰好落在AD上，BE与AC交于点G，连接PF，如图2．

①FG：GA＝▲ ；

②PF与DC的位置关系为▲ ；

③求PQ的长；

(3) 开放拓展

若△EFC绕点C旋转一周，当AC⊥CF时，∠AEC为．

【考点】

旋转的性质; 三角形的综合; 三角形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 问题探究

(1) 如图1，△ABC和△DEC均为等腰直角三角形，∠ACB＝∠DCE＝90°，点B ， D ， E在同一直线上，连接AD ， BD ．

①请探究AD与BD之间的位置关系：；

②若AC＝BC＝ $\text{[math]}$ ，DC＝CE＝ $\text{[math]}$ ，则线段AD的长为；

(2) 拓展延伸

如图2，△ABC和△DEC均为直角三角形，∠ACB＝∠DCE＝90°，AC＝ $\text{[math]}$ ，BC＝ $\text{[math]}$ ，CD＝ $\text{[math]}$ ，CE＝1．将△DCE绕点C在平面内顺时针旋转，设旋转角∠BCD为α（0°≤α＜360°），作直线BD ，连接AD ，当点B ， D ， E在同一直线上时，画出图形，并求线段AD的长．

综合题困难

2. 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D ， E分别为 $\text{[math]}$ ， $\text{[math]}$ 的中点． $\text{[math]}$ 绕点C顺时针旋转，设旋转角为 $\text{[math]}$ （ $\text{[math]}$ ，记直线 $\text{[math]}$ 与直线 $\text{[math]}$ 的交点为点P ．

(1) 如图1，当 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为， $\text{[math]}$ 与 $\text{[math]}$ 的位置关系为；

(2) 当 $\text{[math]}$ 时，上述结论是否成立？若成立，请仅就图2的情形进行证明；若不成立，请说明理由；

(3) $\text{[math]}$ 绕点C顺时针旋转一周，请直接写出运动过程中P点运动轨迹的长度和P点到直线 $\text{[math]}$ 距离的最大值．

综合题困难

3. 综合与实践

问题情境

在综合与实践课上，老师组织同学们以“三角形纸片的旋转”为主题开展数学活动．如图1，现有矩形纸片ABCD ， AB＝4cm ， AD＝3cm ．连接BD ，将矩形ABCD沿BD剪开，得到△ABD和△BCE ．保持△ABD位置不变，将△BCE从图1的位置开始，绕点B按逆时针方向旋转，旋转角为α（0°≤α＜360°）．

(1) 操作发现

在△BCE旋转过程中，连接AE ， AC ，则当α＝0°时， $\text{[math]}$ 的值是；

(2) 如图2，将图1中的△BCE旋转，当点E落在BA延长线上时停止旋转，求出此时的 $\text{[math]}$ 值；

(3) 实践探究

如图3，将图2中的△BCE继续旋转，当AC＝AE时停止旋转，直接写出此时α的度数，并求出△AEC的面积；

(4) 将图3中的△BCE继续旋转，则在某一时刻AC和AE还能相等吗？如果不能，则说明理由；如果能，请在图4中画出此时的△BCE ，连接AC ， AE ，并直接写出△AEC的面积值．

综合题困难