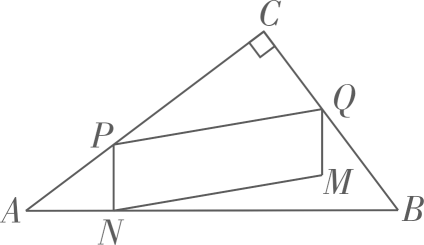
1.
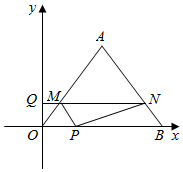
如图,  的顶点坐标分别为
的顶点坐标分别为  ,动点P、Q同时从点O出发,分别沿x轴正方向和y轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点P到达点B时点P、Q同时停止运动.过点Q作
,动点P、Q同时从点O出发,分别沿x轴正方向和y轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点P到达点B时点P、Q同时停止运动.过点Q作  分别交
分别交  、
、  于点M、N,连接
于点M、N,连接  、
、  .设运动时间为t(秒).
.设运动时间为t(秒).
(1)
求点M的坐标(用含t的式子表示);
(2)
求四边形  面积的最大值或最小值;
(3)
是否存在这样的直线l,总能平分四边形
面积的最大值或最小值;
(3)
是否存在这样的直线l,总能平分四边形  的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;
(4)
连接
的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;
(4)
连接  ,当
,当  时,求点N到
时,求点N到  的距离.
的距离.
【考点】
坐标与图形性质;
勾股定理;
平行四边形的判定与性质;
矩形的判定与性质;
相似三角形的判定与性质;
能力提升