1.
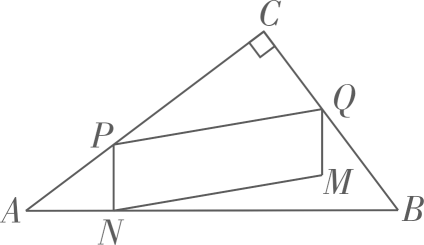
如图,在Rt△ABC中,∠C=90°,AC=20,BC=15。点P从点A出发,沿AC向终点C运动,同时点Q从点C出发,沿射线CB运动,它们的速度均为每秒5个单位长度,点P到达终点时,P、Q同时停止运动。当点P不与点A、C重合时,过点P作PN⊥AB于点N,连结PQ,以PN、PQ为邻边作  PQMN。设
PQMN。设  PQMN与△ABC重叠部分图形的面积为S。点P的运动时间为t秒。
PQMN与△ABC重叠部分图形的面积为S。点P的运动时间为t秒。
(1)
①AB的长为;
(2)
当  PQMN为矩形时,求t的值
(3)
当
PQMN为矩形时,求t的值
(3)
当  PQMN与△ABC重叠部分图形为四边形时,求S与t之间的函数关系式
(4)
当过点P且平行于BC的直线经过
PQMN与△ABC重叠部分图形为四边形时,求S与t之间的函数关系式
(4)
当过点P且平行于BC的直线经过  PQMN一边中点时,直接写出t的值
PQMN一边中点时,直接写出t的值
②PN的长用含t的代数式表示为。
【考点】
勾股定理;
平行四边形的判定与性质;
相似三角形的判定与性质;
能力提升
真题演练