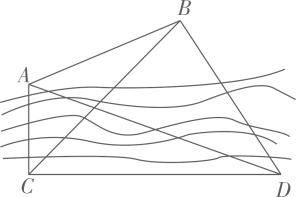
如图，为了测量河对岸两点A，B之间的距离，在河岸这边取点C，D.测得，，，，，设A，B，C，D在同一平面内，求A，B两点之间的距离.（参考数据： .）

0 返回出卷网首页

1. 如图，为了测量河对岸两点A，B之间的距离，在河岸这边取点C，D.测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设A，B，C，D在同一平面内，求A，B两点之间的距离.（参考数据： $\text{[math]}$ .）

【考点】

勾股定理; 正方形的判定与性质; 解直角三角形的其他实际应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 某超大型集装箱船，船身呈长方形，如图所示，长 $\text{[math]}$ 米，宽 $\text{[math]}$ 米，船身和河岸的夹角 $\text{[math]}$ ．河岸 $\text{[math]}$ ，求河岸 $\text{[math]}$ 与 $\text{[math]}$ 之间的距离（结果保留根号）．

解答题容易

2. “醒狮”是岭南文化名城佛山一块闪亮的招牌，是国家非物质文化遗产之一．舞狮者用狮嘴将悬于高处、寓意着吉祥的“生菜”采摘的过程称为“采青”．舞狮者脚站立的位置与狮嘴可触摸到的位置之间的距离称为“采摘距离”．如图，舞狮者站在梅花桩AB上，AB与“生菜”放置点D的水平距离BC为1.1米，LD=53°．已知该舞狮者采摘距离为1.43米，请利用所学知识判断该舞狮者能否“采青”成功，并说明理由．

（参考数据：sin53°~0.8，cos53°~0.6，tan53~1.3）

解答题容易

3. 如图1是一种可折叠的台灯，图2是台灯的结构图， $\text{[math]}$ 是可以绕点A旋转的支架， $\text{[math]}$ 是可以绕点B旋转的支架，C为灯泡的位置．量得 $\text{[math]}$ ，当 $\text{[math]}$ ， $\text{[math]}$ 时，求点C到 $\text{[math]}$ 的距离．（参考数据， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

解答题容易