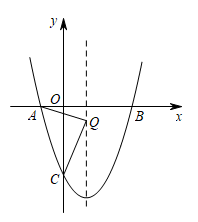1.
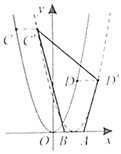
如图,直线  与
与  轴交于点
轴交于点  ,直线
,直线  与
与  轴交于点
轴交于点  ,抛物线
,抛物线  的顶点为
的顶点为  ,且与
,且与  轴左交点为
轴左交点为  (其中
(其中  ).
).
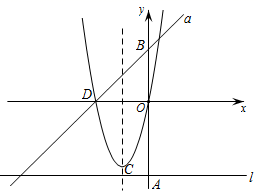
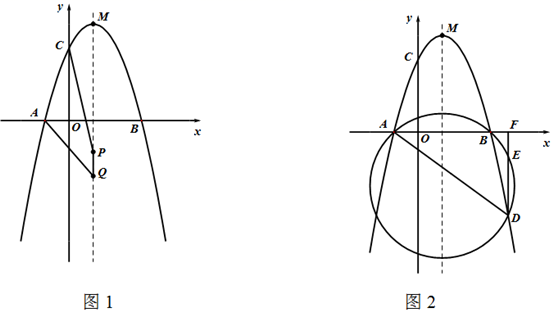
(1)
当  时,在抛物线的对称轴上求一点
时,在抛物线的对称轴上求一点  使得
使得  的周长最小;
(2)
当点
的周长最小;
(2)
当点  在直线
在直线  上方时,求点
上方时,求点  到直线
到直线  距离的最大值;
(3)
若把横坐标、纵坐标都是整数的点称为“整点”.当
距离的最大值;
(3)
若把横坐标、纵坐标都是整数的点称为“整点”.当  时,求出在抛物线和直线
时,求出在抛物线和直线  所围成的封闭图形的边界上的“整点”的个数.
所围成的封闭图形的边界上的“整点”的个数.
【考点】
轴对称的应用-最短距离问题;
二次函数-动态几何问题;
能力提升
真题演练