1.
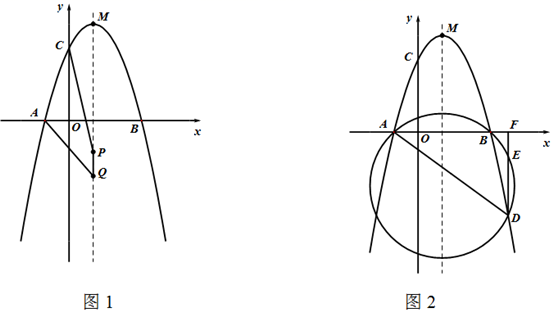
如图,已知点  ,
,  ,两点
,两点  ,
,  在抛物线
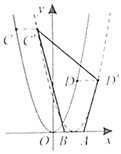
在抛物线  上,向左或向右平移抛物线后,
上,向左或向右平移抛物线后,  ,
,  的对应点分别为
的对应点分别为  ,
,  ,当四边形
,当四边形  的周长最小时,抛物线的解析式为.
的周长最小时,抛物线的解析式为.
【考点】
轴对称的应用-最短距离问题;
二次函数与一次函数的综合应用;
二次函数-动态几何问题;
基础巩固
能力提升
变式训练
拓展培优