1.

(1)
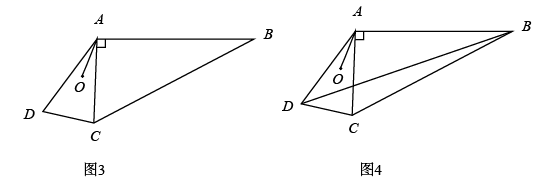
在图①中,若  ,则
,则  的长为
的长为  ;
(2)
如图②,用边长为
;
(2)
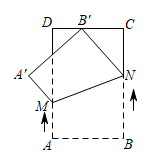
如图②,用边长为  的正方形纸片进行如下操作:对折正方形
的正方形纸片进行如下操作:对折正方形  得折痕
得折痕  ,连接
,连接  ,将
,将  折叠到
折叠到  上,点
上,点  对应点
对应点  ,得折痕
,得折痕  .试说明:
.试说明:  是
是  的黄金分割点;
(3)
如图③,小明进一步探究:在边长为
的黄金分割点;
(3)
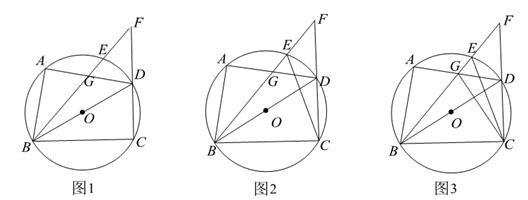
如图③,小明进一步探究:在边长为  的正方形
的正方形  的边
的边  上任取点
上任取点  ,连接
,连接  ,作
,作  ,交
,交  于点
于点  ,延长
,延长  、
、  交于点
交于点  .他发现当
.他发现当  与
与  满足某种关系时,
满足某种关系时,  、
、  恰好分别是
恰好分别是  、
、  的黄金分割点.请猜想小明的发现,并说明理由.
(4)
我们知道:如图①,点
的黄金分割点.请猜想小明的发现,并说明理由.
(4)
我们知道:如图①,点  把线段
把线段  分成两部分,如果
分成两部分,如果  ,那么称点
,那么称点  为线段
为线段  的黄金分割点.它们的比值为.
的黄金分割点.它们的比值为.
【考点】
勾股定理;
相似三角形的判定与性质;
三角形全等的判定-ASA;