1.
在几何探究问题中,经常需要通过作辅助线(如,连接两点,过某点作垂线,作延长线,作平行线等等)把分散的条件相对集中,以达到解决问题的目的.

(1)
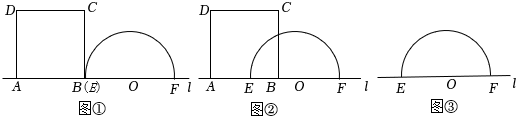
(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上,  ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为(直接写出结果).
(2)
(验证猜想)同学们讨论得出下列三种证明思路(如图1):
(3)
(迁移应用)如图2,点E,F分别在正方形ABCD的边BC,CD上,且
,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为(直接写出结果).
(2)
(验证猜想)同学们讨论得出下列三种证明思路(如图1):
(3)
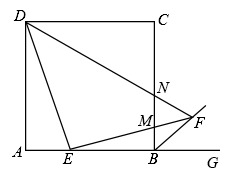
(迁移应用)如图2,点E,F分别在正方形ABCD的边BC,CD上,且  ,
,  ,设
,设  ,试用含
,试用含  的代数式表示DF的长.
的代数式表示DF的长.
思路一:过点A作 ,交CD的延长线于点G.
思路二:过点A作 ,并截取
,连接DG.
思路三:延长CD至点G,使 ,连接AG.
请选择你喜欢的一种思路证明(探究发现)中的结论.
【考点】
三角形全等的判定;
勾股定理;
正方形的性质;
能力提升
真题演练