1.
定义:有三个角相等的四边形叫做三等角四边形.


(1)
在三等角四边形  中,
中,  ,则
,则  的取值范围为;
(2)
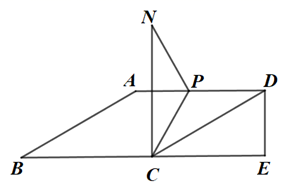
如图1,折叠平行四边形
的取值范围为;
(2)
如图1,折叠平行四边形  ,使得顶点
,使得顶点  分别落在边
分别落在边  上的点
上的点  处,折痕为
处,折痕为  .求证:四边形
.求证:四边形  为三等角四边形;
(3)
如图
为三等角四边形;
(3)
如图  ,在三等角四边形
,在三等角四边形  中,
中,  ,若
,若  ,
,  ,
,  ,则
,则  的长度为.
的长度为.
【考点】
等腰三角形的性质;
勾股定理;
多边形内角与外角;
平行四边形的性质;
翻折变换(折叠问题);