1.
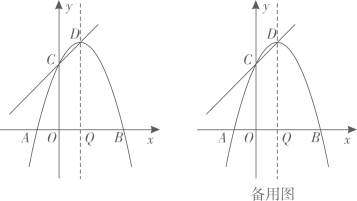
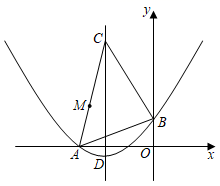
将一张三角形纸片ABC放置在如图所示的平面直角坐标系中,点A(﹣6,0),点B(0,2),点C(﹣4,8),二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,该抛物线的对称轴经过点C,顶点为D.
(1)
求该二次函数的表达式及点D的坐标;
(2)
点M在边AC上(异于点A,C),将三角形纸片ABC折叠,使得点A落在直线AB上,且点M落在边BC上,点M的对应点记为点N,折痕所在直线l交抛物线的对称轴于点P,然后将纸片展开.
①请作出图中点M的对应点N和折痕所在直线l;(要求:尺规作图,不写作法,保留作图痕迹)
②连接MP,NP,在下列选项中:A.折痕与AB垂直,B.折痕与MN的交点可以落在抛物线的对称轴上,C. =
,D.
=
,所有正确选项的序号是 .
③点Q在二次函数y=ax2+bx+c(a≠0)的图象上,当 PDQ∼
PMN时,求点Q的坐标.
【考点】
待定系数法求二次函数解析式;
翻折变换(折叠问题);
相似三角形的性质;
等腰直角三角形;
三角形全等的判定-AAS;