1.
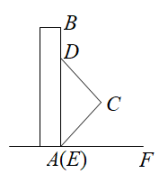
如图,将一块  为
为  的直角三角板
的直角三角板  和等腰直角三角板
和等腰直角三角板  叠合在一起,边
叠合在一起,边  与
与  重合,斜边
重合,斜边  .当点
.当点  从点
从点  出发沿着
出发沿着  方向滑动时,点
方向滑动时,点  同时沿着
同时沿着  方向滑动.当点
方向滑动.当点  从点
从点  滑动到点
滑动到点  时,点
时,点  运动的路径长为.
运动的路径长为.

【考点】
等腰直角三角形;
角平分线的判定;
三角形全等的判定-AAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练