如图，二次函数的图象与一次函数的图象交于点、（点在右侧），与轴交于点，点的横坐标恰好为 .动点、同时从原点出发，沿射线分别以每秒和个单位长度运动，经过秒后，以为对角线作矩形，且矩形四边与坐标轴平行.

0 返回出卷网首页

1. 如图，二次函数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 、 $\text{[math]}$ （点 $\text{[math]}$ 在右侧），与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 的横坐标恰好为 $\text{[math]}$ .动点 $\text{[math]}$ 、 $\text{[math]}$ 同时从原点 $\text{[math]}$ 出发，沿射线 $\text{[math]}$ 分别以每秒 $\text{[math]}$ 和 $\text{[math]}$ 个单位长度运动，经过 $\text{[math]}$ 秒后，以 $\text{[math]}$ 为对角线作矩形 $\text{[math]}$ ，且矩形四边与坐标轴平行.

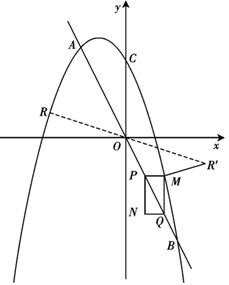
(1) 求 $\text{[math]}$ 的值及 $\text{[math]}$ 秒时点 $\text{[math]}$ 的坐标；

(2) 当矩形 $\text{[math]}$ 与抛物线有公共点时，求时间 $\text{[math]}$ 的取值范围；

(3) 在位于 $\text{[math]}$ 轴上方的抛物线图象上任取一点 $\text{[math]}$ ，作关于原点 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，当点 $\text{[math]}$ 恰在抛物线上时，求 $\text{[math]}$ 长度的最小值，并求此时点 $\text{[math]}$ 的坐标.

【考点】

二次函数的最值; 勾股定理; 关于原点对称的点的坐标特征; 二次函数与一次函数的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知二次函数y=-(x-m)²+m

(1) 写出该函数图象顶点的坐标及其所在直线的函数表达式。

(2) 若该函数图象的顶点在第一象限，试判断该函数图象与x轴的交点个数并说明理由。

(3) 若在-2≤x≤2范围内，若图象上的点到x轴的距离最小值为2，求m的值。

综合题普通

2. 在平面直角坐标系中，一次函数y=x+3的图象与x轴交于点A，二次函数y=x²+mx+n的图象经过点A．

(1) 当m=4时，求n的值；

(2) 设m=﹣2，当﹣3≤x≤0时，求二次函数y=x²+mx+n的最小值；

(3) 当﹣3≤x≤0时，若二次函数﹣3≤x≤0时的最小值为﹣4，求m、n的值．

综合题普通

3. 如图，抛物线y=ax²+bx+ $\text{[math]}$ 与直线AB交于点A（﹣1，0），B（4， $\text{[math]}$ ），点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD

(1) 求抛物线的解析式

(2) 设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出当S取最大值时的点C的坐标

综合题普通