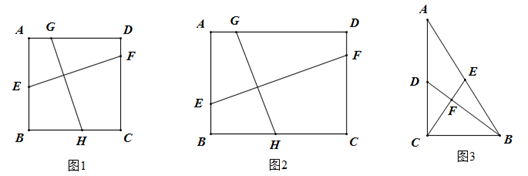
1.
如果三角形的两个内角  与
与  满足
满足  ,那么我们称这样的三角形为“准互余三角形”.
,那么我们称这样的三角形为“准互余三角形”.
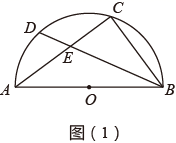
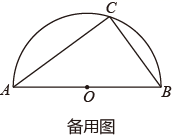
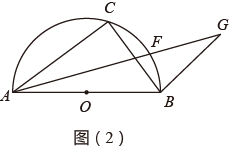
(1)
若  是“准互余三角形”,
是“准互余三角形”,  ,则
,则  .
(2)
如图(1),
.
(2)
如图(1),  是半圆的直径,
是半圆的直径,  是半圆上的点,D是
是半圆上的点,D是  上的点,
上的点,  交
交  于点E.
于点E.
①若D是 的中点,则图中共有 ▲ 个“准互余三角形”;
②当 是“准互余三角形”时,求
的长;
③如图(2)所示,若F是 上的点(不与
重合),G为射线
上一点,且满足
.当
是“准互余三角形”时,求
的长.
【考点】
勾股定理;
圆周角定理;
翻折变换(折叠问题);
相似三角形的判定与性质;
三角形全等的判定-AAS;
能力提升