如图

0 返回出卷网首页

1. 如图

(1) 【基础巩固】

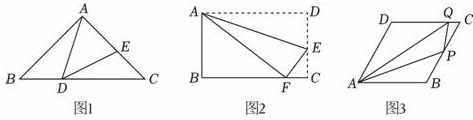
如图1，点A，F，B在同一直线上，若∠A＝∠B＝∠EFC，求证：△AFE∼△BCF；

(2) 【尝试应用】

如图2，AB是半圆⊙O的直径，弦长AC＝BC＝4 $\text{[math]}$ ，E，F分别是AC，AB上的一点，∠CFE＝45°，若设AE＝y，BF＝x，求出y与x的函数关系及y的最大值.

(3) 【拓展提高】

已知D是等边△ABC边AB上的一点，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上.如图3，如果AD：BD＝1：2，求CE：CF的值.

【考点】

等腰三角形的性质; 等边三角形的性质; 勾股定理; 翻折变换（折叠问题）; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 如图1，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是线段 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ．

(1) 填空：

① $\text{[math]}$ 的值为；

② $\text{[math]}$ 的度数为．

(2) 类比探究

如图2，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是线段 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ．请求出 $\text{[math]}$ 的值及 $\text{[math]}$ 的度数，并说明理由．

实践探究题普通

2. 问题提出：

(1) 如图1，在等腰直角△ABC中，∠BAC＝90°，AB＝AC ，点D、E分别在边BC、AC上，连接AD、DE ，有∠ADE＝45°．求证：△BDA∽△CED；

(2) 问题探究

如图2，将矩形ABCD沿AE折叠，使点D落在BC边的点F处，若AB＝3，AD＝5，求DE的长；

(3) 问题解决

如图3，菱形ABCD是一座避暑山庄的平面示意图，其中∠BAD＝60°，AB＝120米，现计划在山庄内修建一个三角形花园AP ，点P、Q分别在线段BC、CD上，根据设计要求要使∠APQ＝120°，且AP＝3PQ ，问能否建造出符合要求的三角形花园APQ ，若能，请找出点P、Q的位置（即求出DQ与BP的长），若不能，请说明理由．

实践探究题普通

3. 如图

[问题背景]

如图1．数学实践课上，学习小组进行探究活动，老师要求大家对矩形ABCD进行如下操作；①分别以点B． C 为圆心，以大于 $\text{[math]}$ BC的长度为半径作弧，两弧相交于点E、F，作真线EF交BC于点O．连接AO；②将△ABO沿AO翻折，点B的对应点落在点P处，作射线AP交CD于点Q．

[问题提出]

在矩形ABCD中，AD=5，AB=3，求线段CQ的长：

[问题解决]

经过小组合作、探究、展示，其中的两个方案如下：

方案一：连按OQ，如图2．经过推理、计算可求出线段CQ的长：

方案二：将△ABO绕点O旋转180°至△RCO处，如图3．经过推理、计算可求出线段CQ的长．

请你任选其中一种方案求线段CQ的长．

实践探究题困难