1.
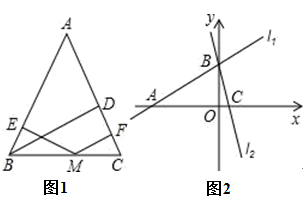
大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式，这种解决问题的方法我们称之为面积法．学有所用：在等腰三角形ABC中，AB＝AC ， 其一腰上的高为h ， M是底边BC上的任意一点，M到腰AB、AC的距离分别为h1、h2 ．
(1)
请你结合图1来证明：h1+h2＝h；
(2)
当点M在BC延长线上时，h1、h2、h之间又有什么样的结论．请你直接写出结论不必证明；
(3)
利用以上结论解答，如图2在平面直角坐标系中有两条直线l1：y＝ 
x+3，l2：y＝﹣3x+3，若l2上的一点M到l1的距离是 
．求点M的坐标．
【考点】
三角形的面积;
等腰三角形的性质;
勾股定理;
一次函数图象与坐标轴交点问题;
