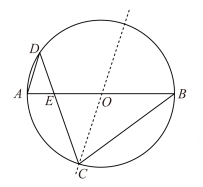
如果一个等腰三角形是2倍角三角形，则其底角的度数为；

小思同学通过从“特殊到一般”的过程，对2倍角三角形进行研究，得出结论：

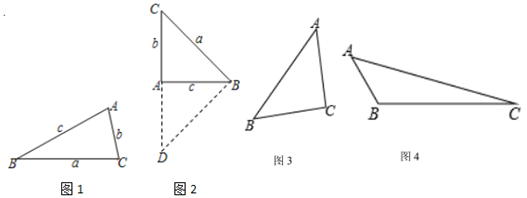
如图1，在△ABC中，如果∠A＝2∠B，那么BC²＝AC（AB＋AC）.

下面是小思同学对其中一种特殊情形的证明方法.

已知：如图2，在△ABC中，∠A＝90°，∠B＝45°.

求证：BC²＝AC（AB＋AC）.

证明：如图2，延长CA到D，使得AD＝AB，连接BD.

∴∠D＝∠ABD，AB＋AC＝AD＋AC＝CD

∵∠CAB＝∠D＋∠ABD＝2∠D，∠CAB＝90°

∴∠D＝45°，

∵∠ABC＝45°，

∴∠D＝∠ABC，又∠C＝∠C

∴△ABC∽△BCD

∴

∴BC²＝AC•CD

∴BC²＝AC（AB＋AC）

根据上述材料提供的信息，请你完成下列情形的证明：

已知：如图1，在△ABC中，∠A＝2∠B.

求证：BC²＝AC（AB＋AC）.

证明：

已知：如图3，在△ABC中，∠C＝2∠B，AB＝12，BC＝10，则AC＝；

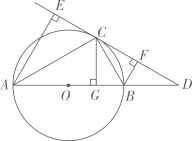
已知：如图4，在△ABC中，∠ABC＝3∠A，AC＝6，BC＝4，求AB的长.