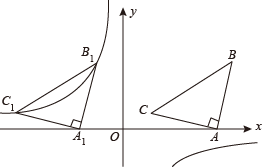
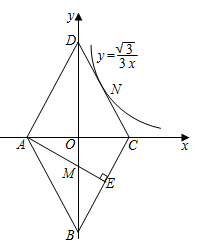
如图，在直角坐标系中，第一象限内的点，都在反比例函数的图象上，横坐标分别是和，点在轴的正半轴上，满足 .且，则的值是.

0 返回出卷网首页

1. 如图，在直角坐标系中，第一象限内的点 $\text{[math]}$ ， $\text{[math]}$ 都在反比例函数的图象上，横坐标分别是 $\text{[math]}$ 和 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，满足 $\text{[math]}$ .且 $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

【考点】

反比例函数图象上点的坐标特征; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题困难

1. 我们把直角坐标系中横坐标与纵坐标都是整数的点称为整点．反比例函数 $\text{[math]}$ 的图象上有一些整点，请写出其中一个整点的坐标．

填空题容易

2. 已知点 $\text{[math]}$ ， $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ $\text{[math]}$ ．（填“＞”，“＜”或“＝”）

填空题容易

3. 若反比例函数 $\text{[math]}$ 经过点 $\text{[math]}$ 和点 $\text{[math]}$ ，则 $\text{[math]}$ ．

填空题容易