0 返回出卷网首页
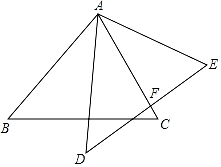
1. 如图，在Rt△ABC中，∠BAC＝90°，∠ACB＝30°，将△ABC绕点C逆时针旋转60°得到△CDE，点A、B的对应点分别是D、E，点F是边BC中点，连结AD、EF．

(1) 求证：△ACD是等边三角形；
(2) 判断AD与EF有怎样的数量关系，并说明理由．
【考点】
等边三角形的判定; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在Rt△OAB中，∠OAB=90。 ， OA=AB=6，将△OAB绕点O沿逆时针方向旋转90。得到△OA1B1 ．

(1) 求线段OA1的长及∠AOB1；
(2) 连接AA1 ， 求四边形OAA1B1的面积．
综合题 普通
2. 如图：△ABC绕点A逆时针方向旋转得到△ADE，其中∠B＝50°，∠C＝60°．

(1) 若AD平分∠BAC时，求∠BAD的度数．
(2) 若AC⊥DE时，AC与DE交于点F，求旋转角的度数．
综合题 普通
3. 如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，连接OD，OA．

(1) 求∠ODC的度数；
(2) 试判断AD与OD的位置关系，并说明理由；
(3) 若OB＝2，OC＝3，求AO的长（直接写出结果）．
综合题 普通