1.
已知:抛物线 经过
经过 ,
,  ,
,  三点.
三点.
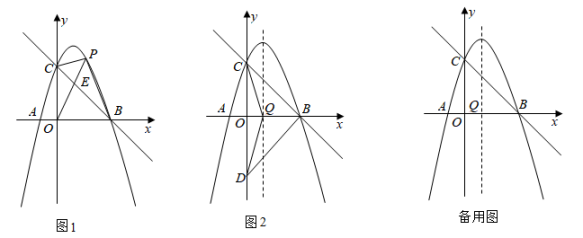
(1)
求抛物线的解析式;
(2)
如图1,点 为直线
为直线 上方抛物线上任意一点,连
上方抛物线上任意一点,连 、
、 、
、 ,
,  交直线
交直线 于点
于点 , 设
, 设 , 求当
, 求当 取最大值时点P的坐标,并求此时
取最大值时点P的坐标,并求此时 的值;
(3)
如图2,点Q为抛物线对称轴与
的值;
(3)
如图2,点Q为抛物线对称轴与 轴的交点,点
轴的交点,点 关于
关于 轴的对称点为点D.
轴的对称点为点D.
①求的周长及
的值;
②点M是y轴负半轴上的点,且满足(
为大于0的常数),求点M的坐标.
【考点】
待定系数法求二次函数解析式;
勾股定理;
相似三角形的判定与性质;
锐角三角函数的定义;
二次函数图象上点的坐标特征;
能力提升



