如图，平面直角坐标系中，四边形OABC为矩形，点A，B的坐标分别为（4，0），（4，3），动点M，N分别从O，B同时出发.以每秒1个单位的速度运动.其中，点M沿OA向终点A运动，点N沿BC向终点C运动.过点M作MP⊥OA，交AC于P，连接NP，已知动点运动了x秒.

0 返回出卷网首页

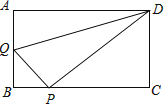
1. 如图，平面直角坐标系中，四边形OABC为矩形，点A，B的坐标分别为（4，0），（4，3），动点M，N分别从O，B同时出发.以每秒1个单位的速度运动.其中，点M沿OA向终点A运动，点N沿BC向终点C运动.过点M作MP⊥OA，交AC于P，连接NP，已知动点运动了x秒.

(1) P点的坐标为多少（用含x的代数式表示）；

(2) 试求△NPC面积S的表达式，并求出面积S的最大值及相应的x值；

(3) 当x为何值时，△NPC是一个等腰三角形？简要说明理由.

【考点】

二次函数的最值; 三角形的面积; 等腰三角形的性质; 矩形的性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在矩形ABCD中，AB＝3cm，BC＝4cm.设P，Q分别为BD，BC上的动点，在点P自点D沿DB方向作匀速移动的同时，点Q自点B沿BC方向向点C作匀速移动，移动的速度均为1cm/s，设P，Q移动的时间为t秒（0＜t≤4）.

(1) 写出△PBQ的面积S（cm²）与时间t（s）的函数关系式，当t为何值时，S有最大值，最大值是多少？

(2) 当t为何值时，△PBQ为等腰三角形？

综合题困难

2. 在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0＜x≤3），解答下列问题：

(1) 设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最大值？并求出最小值；

(2) 是否存在x的值，使得QP⊥DP？试说明理由．

综合题困难

3. 在矩形ABCD中，AB=a，AD=b，点M为BC边上一动点（点M与点B、C不重合），连接AM，过点M作MN⊥AM，垂足为M，MN交CD或CD的延长线于点N．

(1) 求证：△CMN∽△BAM；

(2) 设BM=x，CN=y，求y关于x的函数解析式．当x取何值时，y有最大值，并求出y的最大值；

(3) 当点M在BC上运动时，求使得下列两个条件都成立的b的取值范围：①点N始终在线段CD上，②点M在某一位置时，点N恰好与点D重合．

综合题困难