1.
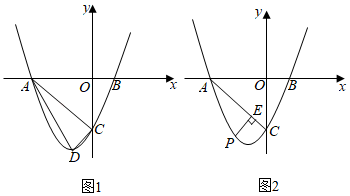
如图1,在平面直角坐标系中,已知B点坐标为(1,0),且OA=OC=3OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点,其中D点是该抛物线的顶点.
(1)
求抛物线的解析式;
(2)
判断△ADC的形状并且求△ADC的面积;
(3)
如图2,点P是该抛物线第三象限部分上的一个动点,过P点作PE⊥AC于E点,当PE的值最大时,求此时P点的坐标及PE的最大值.
【考点】
二次函数的最值;
待定系数法求二次函数解析式;
勾股定理的逆定理;
锐角三角函数的定义;
坐标系中的两点距离公式;