如图，在矩形ABCD中，AB＝8，AD＝4，点P是对角线BD上一点，连接AP，AE⊥AP，且＝，连接BE．

0 返回出卷网首页

1. 如图，在矩形ABCD中，AB＝8，AD＝4，点P是对角线BD上一点，连接AP，AE⊥AP，且 $\text{[math]}$ ＝ $\text{[math]}$ ，连接BE．

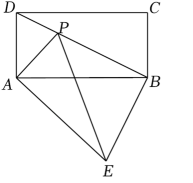
(1) 当DP＝2时，求BE的长．

(2) 四边形AEBP可能为矩形吗？如果不可能，请说明理由；如果可能，求出此时四边形AEBP的面积．

【考点】

勾股定理; 矩形的性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在矩形ABCD中，AB = 6，AD = 8，点E是CD边上的一个动点（点E不与点C重合），延长DC到点F，使EC = 2CF，且AF与BE交于点G.

(1) 当EC = 4时，求线段BG的长：

(2) 设CF = x，△GEF的面积为y，求y与x的关系式，并求出y的最大值：

(3) 连接DG，求线段DG的最小值.

综合题困难

2. 矩形 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 交于点O， $\text{[math]}$ （k为常数）．作 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别与 $\text{[math]}$ 、 $\text{[math]}$ 边相交于点E、F，连接 $\text{[math]}$ ，

(1) 发现问题：如图1，若 $\text{[math]}$ ，猜想： $\text{[math]}$ ；

(2) 类比探究：如图2， $\text{[math]}$ ，探究线段 $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并说明理由；

(3) 拓展运用：如图3，在（2）的条件下，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题困难

3. 如图，在平面直角坐标系中，矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上，OC=8，OE=17，抛物线y= $\text{[math]}$ x²﹣3x+m与y轴相交于点A，抛物线的对称轴与x轴相交于点B，与CD交于点K．

(1) 将矩形OCDE沿AB折叠，点O恰好落在边CD上的点F处．

①点B的坐标为（、），BK的长是，CK的长是；

②求点F的坐标；

③请直接写出抛物线的函数表达式；

(2) 将矩形OCDE沿着经过点E的直线折叠，点O恰好落在边CD上的点G处，连接OG，折痕与OG相交于点H，点M是线段EH上的一个动点（不与点H重合），连接MG，MO，过点G作GP⊥OM于点P，交EH于点N，连接ON，点M从点E开始沿线段EH向点H运动，至与点N重合时停止，△MOG和△NOG的面积分别表示为S₁和S₂ ，在点M的运动过程中，S₁•S₂（即S₁与S₂的积）的值是否发生变化？若变化，请直接写出变化范围；若不变，请直接写出这个值．

综合题困难