如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，OD∥BC交AC相交于点E．

0 返回出卷网首页

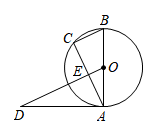
1. 如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，OD∥BC交AC相交于点E．

(1) 若AC=2CB，求证：△ABC≌△DAE；

(2) 若AB=6，OD=8，求BC的长．

【考点】

三角形全等的判定; 切线的性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在△ABC中，CD平分∠ACB，且AD＝BD．

(1) 若AC＝6，BC＝8，AB＝10，求∠ACD的度数；

(2) 证明：∠ACB+∠ADB=180°；

(3) 设 $\text{[math]}$ ，试判断CA，CD，CB之间的数量关系（用含k的式子表示），并说明理由．

综合题困难

2. 在四边形ABCD中，对角线AC，BD交于点O，AC平分∠BAD，∠BAC＝∠CBD，AC＝AD．

① $\text{[math]}$ ；

② $\text{[math]}$ ；

(2) 当∠BAD＝90°时，求 $\text{[math]}$ 的值．

综合题困难

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D是 $\text{[math]}$ 的中点，点O是AB上一点，以点O为圆心、 $\text{[math]}$ 为半径作 $\text{[math]}$ ，与AB相交于点F，与 $\text{[math]}$ 相切于点E，连接BD与 $\text{[math]}$ 相交于点G．

(1) 求证：BE平 $\text{[math]}$ ；

(2) 当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长．

综合题普通