1.
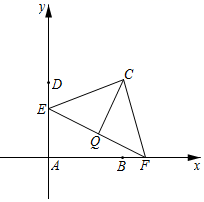
如图,在△ABC中,∠ACB=90°,AC=12,BC=9,点D为边AB的中点.点P从点A出发,沿AC方向以每秒1个单位的速度向终点C运动;同时点Q从点C出发,以每秒2个单位的速度沿CB方向运动,以DP、DQ为邻边构造平行四边形PEQD.设点P运动的时间为t秒, .
.

(1)
求当t为何值时, ?
(2)
设平行四边形PEQD的面积为S(
?
(2)
设平行四边形PEQD的面积为S( ),求S关于t之间的函数关系式;
(3)
连接CD,是否存在某一时刻t,CD经过平行四边形PEQD的对称中心O?若存在,求出t的值;若不存在,请说明理由;
),求S关于t之间的函数关系式;
(3)
连接CD,是否存在某一时刻t,CD经过平行四边形PEQD的对称中心O?若存在,求出t的值;若不存在,请说明理由;
【考点】
几何图形的面积计算-割补法;
三角形的综合;
三角形-动点问题;
能力提升
真题演练