如图，在菱形ABCD中，AB=3，∠B=60°，AC为对角线，点E、F分别在边AB、BC上（不与端点重合），且AE=BF，连接CE、AF交于点G.

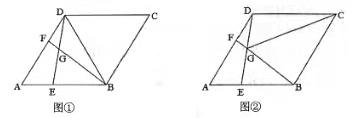
1. 如图，在菱形ABCD中，AB=3，∠B=60°，AC为对角线，点E、F分别在边AB、BC上（不与端点重合），且AE=BF，连接CE、AF交于点G.

(1) 求证：△ABF≌△CAE；

(2) 求∠FGC的度数；

(3) 连接EF，DG，若EF⊥BC，求线段DG的长.

【考点】

等边三角形的判定与性质; 菱形的性质; 相似三角形的判定与性质; 锐角三角函数的定义; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是对角线 $\text{[math]}$ 上一点． $\text{[math]}$ 是线段 $\text{[math]}$ 延长线上一点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ．

综合题困难

综合题普通

①如图2，若BM＝MN，过点A作AD∥BC交CN的延长线于点D，求DN∶CN的值；

②如图3，若BM＞MN，延长BN至点E，使BM＝ME，过点A作AF∥BC交CE的延长线于点F，若E是CF的中点，且CN＝1，直接写出线段AF的长.

综合题普通