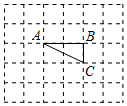
如图，在边长为1个单位长度的网格中，建立平面直角坐标系顶点均在格点上的三角形，我们称作格点三角形．

0 返回出卷网首页

1. 如图，在边长为1个单位长度的 $\text{[math]}$ 网格中，建立平面直角坐标系顶点均在格点上的三角形，我们称作格点三角形．

(1) $\text{[math]}$ 的面积为， $\text{[math]}$ 中 $\text{[math]}$ 边上的高为；

(2) 画出将 $\text{[math]}$ 绕原点旋转180°后得到的 $\text{[math]}$ ，并直接写出点 $\text{[math]}$ 的坐标．

【考点】

三角形的面积; 作图﹣旋转;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．

问题引入：

(1) 如图①，当点D是BC边上的中点时，S_△_ABD：S_△_ABC=；当点D是BC边上任意一点时，S_△_ABD：S_△_ABC=（用图中已有线段表示）．

(2) 如图②，在△ABC中，O点是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S_△_BOC与S_△_ABC之比应该等于图中哪两条线段之比，并说明理由．

(3) 如图③，O是线段AD上一点（不与点A、D重合），连结BO并延长交AC于点F，连结CO并延长交AB于点E，试猜想 $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ 的值，并说明理由．

综合题普通

2. 如图，点D双曲线上，AD垂直x轴，垂足为A，点C在AD上，CB平行于x轴交曲线于点B，直线AB与y轴交于点F，已知AC：AD=1：3，点C的坐标为（2，2）．

(1) 求该双曲线的解析式；

(2) 求△OFA的面积．

综合题普通

3. 探究证明：

(1) 如图1，在△ABC中，AB=AC，点E是BC上的一个动点，EG⊥AB，EF⊥AC，CD⊥AB，点G，F，D分别是垂足．求证：CD=EG+EF；

猜想探究：

(2) 如图2，在△ABC中，AB=AC，点E是BC的延长线上的一个动点，EG⊥AB于G，EF⊥AC交AC延长线于F，CD⊥AB于D，直接猜想CD、EG、EF之间的关系为；

(3) 如图3，边长为10的正方形ABCD的对角线相交于点O、H在BD上，且BH=BC，连接CH，点E是CH上一点，EF⊥BD于点F，EG⊥BC于点G，则EF+EG=．

综合题普通