如图，BE是⊙O直径，点A是⊙O外一点：OA⊥OB，AP切⊙O于点P，连接BP交AO于点C．

0 返回出卷网首页

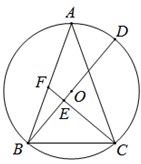
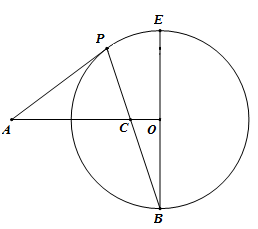
1. 如图，BE是⊙O直径，点A是⊙O外一点：OA⊥OB，AP切⊙O于点P，连接BP交AO于点C．

(1) 求证：∠PAO=2∠PBO；

(2) 若⊙O的半径为5， $\text{[math]}$ ，求BP的长．

【考点】

勾股定理; 圆周角定理; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，△ABC内接于⊙O，AB=AC，CF垂直直径BD于点E，交边AB于点F.

(1) 求证：∠BFC=∠ABC.

(2) 若⊙O的半径为5，CF=6，求AF长.

综合题普通

2. 如图，在每个小正方形的边长为 $\text{[math]}$ 的网格中，点 $\text{[math]}$ ，点 $\text{[math]}$ 均落在格点上， $\text{[math]}$ 为⊙ $\text{[math]}$ 的直径．

(1) $\text{[math]}$ 的长等于；

(2) 请在如图所示的网格中，用无刻度的直尺，画出一个以 $\text{[math]}$ 为斜边、面积为 $\text{[math]}$ 的 $\text{[math]}$ ，并简要说明点 $\text{[math]}$ 的位置是如何找到的（不要求证明）．

综合题普通

3. 如图，点 $\text{[math]}$ 和动点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，点 $\text{[math]}$ 关于点 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，以 $\text{[math]}$ 为边作 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ ，作 $\text{[math]}$ 的外接圆 $\text{[math]}$ .点 $\text{[math]}$ 在点 $\text{[math]}$ 右侧， $\text{[math]}$ ，过点 $\text{[math]}$ 作直线 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 右侧的圆弧于点 $\text{[math]}$ .在射线 $\text{[math]}$ 上取点 $\text{[math]}$ ，使 $\text{[math]}$ ，以 $\text{[math]}$ ， $\text{[math]}$ 为邻边作矩形 $\text{[math]}$ .设 $\text{[math]}$ .

(1) 用关于 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ， $\text{[math]}$ .

(2) 当点 $\text{[math]}$ 在点 $\text{[math]}$ 右侧时，若矩形 $\text{[math]}$ 的面积等于90，求 $\text{[math]}$ 的长.

(3) 当点 $\text{[math]}$ 在点 $\text{[math]}$ 右侧时，作直线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ 的弦心距为1，求 $\text{[math]}$ 的长.

综合题困难