1.
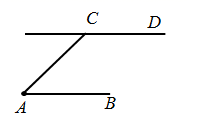
如图,点  和动点
和动点  在直线
在直线  上,点
上,点  关于点
关于点  的对称点为
的对称点为  ,以
,以  为边作
为边作  ,使
,使  ,
,  ,作
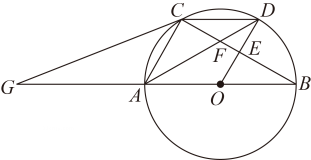
,作  的外接圆
的外接圆  .点
.点  在点
在点  右侧,
右侧,  ,过点
,过点  作直线
作直线  ,过点
,过点  作
作  于点
于点  ,交
,交  右侧的圆弧于点
右侧的圆弧于点  .在射线
.在射线  上取点
上取点  ,使
,使  ,以
,以  ,
,  为邻边作矩形
为邻边作矩形  .设
.设  .
.

(1)
用关于  的代数式表示
的代数式表示  ,
,  .
(2)
当点
.
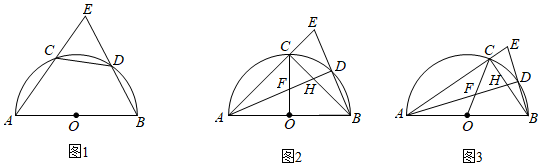
(2)
当点  在点
在点  右侧时,若矩形
右侧时,若矩形  的面积等于90,求
的面积等于90,求  的长.
(3)
当点
的长.
(3)
当点  在点
在点  右侧时,作直线
右侧时,作直线  交
交  于点
于点  ,若
,若  的弦心距为1,求
的弦心距为1,求  的长.
的长.
【考点】
勾股定理;
圆周角定理;