1.
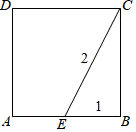
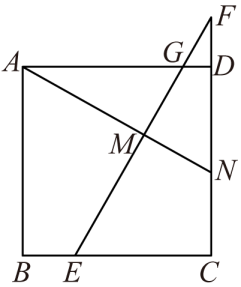
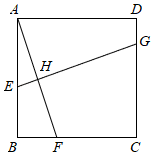
如图,正方形  中,E、F分别为边
中,E、F分别为边  上的点,且
上的点,且  ,过F作
,过F作  ,交
,交  于G,过H作
于G,过H作  于M,若
于M,若  ,则下列结论中:
,则下列结论中:
① ;②
;③
,其中结论正确的是( )

A.
只有①②
B.
只有①③
C.
只有②③
D.
①②③
【考点】
勾股定理;
正方形的性质;
四边形的综合;
基础巩固
能力提升
变式训练
拓展培优
真题演练