1.
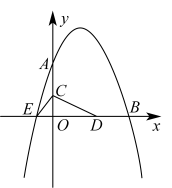
如图所示,在平面直角坐标系中,抛物线  经过
经过  、
、  、
、  三点,其顶点为
三点,其顶点为  ,连接
,连接  ,点
,点  是线段
是线段  上一个动点(不与
上一个动点(不与  、
、  重合),过点
重合),过点  作
作  轴的垂线,垂足点为
轴的垂线,垂足点为  ,连接
,连接  .
.

(1)
求抛物线的函数解析式,并写出顶点  的坐标:
(2)
如果
的坐标:
(2)
如果  点的坐标为
点的坐标为  ,
,  的面积为
的面积为  ,求
,求  与
与  之间的函数关系式,直接写出自变量
之间的函数关系式,直接写出自变量  的取值范围,并求出
的取值范围,并求出  的最大值;
的最大值;
【考点】
待定系数法求二次函数解析式;
三角形的面积;
二次函数与一次函数的综合应用;
能力提升
真题演练