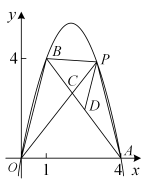
在平面直角坐标系xOy中，已知抛物线经过A（4，0），B（1，4）两点.P是抛物线上一点，且在直线AB的上方.

0 返回出卷网首页

1. 在平面直角坐标系xOy中，已知抛物线 $\text{[math]}$ 经过A（4，0），B（1，4）两点.P是抛物线上一点，且在直线AB的上方.

(1) 求抛物线的解析式；

(2) 若△OAB面积是△PAB面积的2倍，求点P的坐标；

(3) 如图，OP交AB于点C， $\text{[math]}$ 交AB于点D.记△CDP，△CPB，△CBO的面积分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .判断 $\text{[math]}$ 是否存在最大值.若存在，求出最大值；若不存在，请说明理由.

【考点】

二次函数的最值; 待定系数法求二次函数解析式; 三角形的面积; 相似三角形的判定与性质; 二次函数与一次函数的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 和 $\text{[math]}$ 两点，直线 $\text{[math]}$ 与x轴相交于点C，P是直线 $\text{[math]}$ 上方的抛物线上的一个动点， $\text{[math]}$ 轴交 $\text{[math]}$ 于点D.

(1) 求该抛物线的表达式；

(2) 若 $\text{[math]}$ 轴交 $\text{[math]}$ 于点E，求 $\text{[math]}$ 的最大值；

(3) 若以A，P，D为顶点的三角形与 $\text{[math]}$ 相似，请直接写出所有满足条件的点P，点D的坐标.

综合题困难

2. 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 相交于 $\text{[math]}$ 两点.

(1) 求c的值；

(2) 在直线 $\text{[math]}$ 上找一点M，使 $\text{[math]}$ ，并求出点M的坐标；

(3) 在线段AB下方的抛物线上是否存在点N，使 $\text{[math]}$ 的面积最大？若存在，求出点N的坐标；若不存在，请说明理由.

综合题困难

3. 如图， $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴的正半轴交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交抛物线于另一点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的负半轴上，连接 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，若 $\text{[math]}$ ．

(1) 用含 $\text{[math]}$ 的代数式表示 $\text{[math]}$ 的长；

(2) 当 $\text{[math]}$ 时，判断点 $\text{[math]}$ 是否落在抛物线上，并说明理由；

(3) 过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，延长 $\text{[math]}$ 至 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，若 $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积相等，求 $\text{[math]}$ 的值．

综合题困难