1.
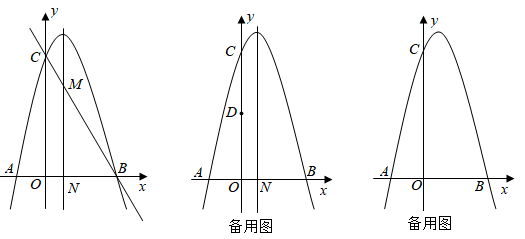
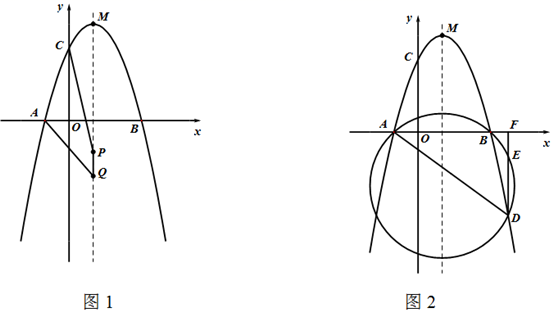
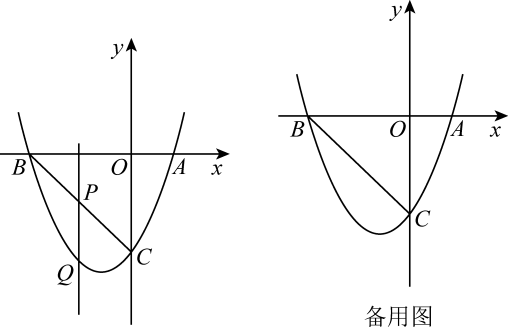
抛物线y=ax2+2x+c与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,6),点D(m,0)是x轴上一点,过点D作直线DF⊥x轴,交直线BC于点E,交抛物线于点F.

(1)
求抛物线的解析式;
(2)
如图,连接BF,当tan∠FBC=  时,求出点E的坐标;
(3)
当△CEF是等腰三角形时,请直接写出点F的坐标.
时,求出点E的坐标;
(3)
当△CEF是等腰三角形时,请直接写出点F的坐标.
【考点】
待定系数法求二次函数解析式;
二次函数与一次函数的综合应用;
二次函数-动态几何问题;
能力提升
真题演练

 备用图
备用图