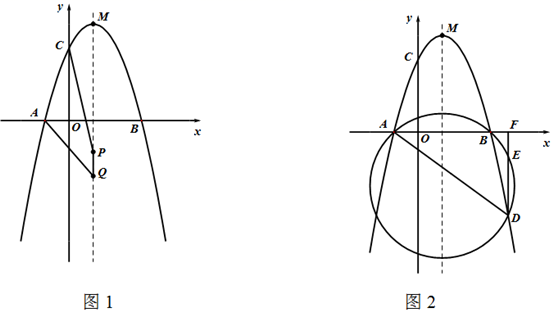
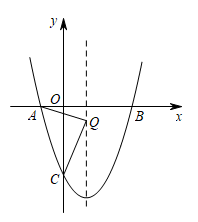1.
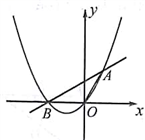
已知抛物线 与
与 轴交于点
轴交于点 和点
和点 , 且过点
, 且过点 .
.
(1)
求该抛物线的解析式及其对称轴;
(2)
连接 , 若抛物线上有一点
, 若抛物线上有一点 满足
满足 , 求点
, 求点 的坐标;
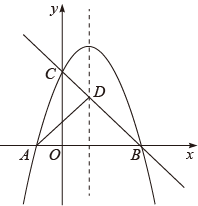
(3)
若点
的坐标;
(3)
若点 是
是 轴上一点,过点
轴上一点,过点 作抛物线对称轴的垂线,垂足为
作抛物线对称轴的垂线,垂足为 , 连接
, 连接 ,
,  , 当
, 当 取最小值时,求点
取最小值时,求点 的坐标及这个最小值.
的坐标及这个最小值.
【考点】
待定系数法求二次函数解析式;
轴对称的应用-最短距离问题;
二次函数-动态几何问题;
能力提升
真题演练