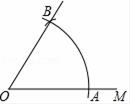
如图，AB是半圆O的直径，以弦AC为折痕折叠后，恰好经过点O，则等于（）

0 返回出卷网首页

1. 如图，AB是半圆O的直径，以弦AC为折痕折叠 $\text{[math]}$ 后，恰好经过点O，则 $\text{[math]}$ 等于（）

A. 120° B. 125° C. 130° D. 145°

【考点】

等边三角形的判定与性质; 翻折变换（折叠问题）;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，已知∠MON及其边上一点A ．以点A为圆心，AO长为半径画弧，分别交OM ， ON于点B和C ．再以点C为圆心，AC长为半径画弧，恰好经过点B ．错误的是（）

A. S_△AOC＝S_△ABC B. ∠OCB＝90° C. ∠MON＝30° D. OC＝2BC

单选题容易

2. 如图，已知 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边上一点， $\text{[math]}$ ，点 $\text{[math]}$ 为线段 $\text{[math]}$ 的中点，以点 $\text{[math]}$ 为圆心，线段 $\text{[math]}$ 长为半径作弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A. 5 B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，已知射线OM，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以点A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，那么∠AOB的度数是（）

A. 90° B. 60° C. 45° D. 30°

单选题容易