在△ ABC中，∠BAC=90° ，AB=AC= ，D为 BC的中点，E，F分别为AC， AD 上任意一点，连接EF，将线段EF绕点E顺时针旋转 90°得到线段EG，连接FG， AG．

0 返回出卷网首页

1. 在△ ABC中，∠BAC=90° ，AB=AC= $\text{[math]}$ ，D为 BC的中点，E，F分别为AC， AD 上任意一点，连接EF，将线段EF绕点E顺时针旋转 90°得到线段EG，连接FG， AG．

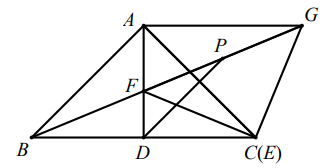
(1) 如图1，点 E 与点 C 重合，且 GF 的延长线过点 B ，若点 P 为 FG 的中点，连接 PD，求 PD的长；

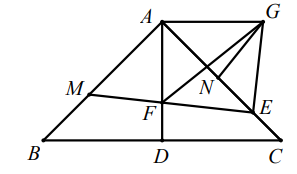
(2) 如图 2，EF 的延长线交 AB 于点M，点N在 AC上， ∠AGN=∠AEG 且GN=MF，求证：AM+AF= $\text{[math]}$ AE

(3) 如图3，F为线段 AD上一动点，E为 AC的中点，连接BE，H为直线BC上一动点，连接 EH，将△ BEH沿EH翻折至△ABC所在平面内，得到△ B'EH'，连接 B'G，直接写出线段 B'G的长度的最小值

【考点】

三角形全等的判定; 翻折变换（折叠问题）; 旋转的性质; 等腰直角三角形; 圆-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知△ABC中，∠C=90°，AC=BC= $\text{[math]}$ ，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B．

(1) 请你在图中把图补画完整；

(2) 求C′B的长．

综合题普通

2. 九年级一班同学在数学老师的指导下，以“等腰三角形的旋转”为主题，开展数学探究活动.

(1) 操作探究：如图1， $\text{[math]}$ 为等腰三角形， $\text{[math]}$ ，将 $\text{[math]}$ 绕点O旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， F是AE的中点，连接 $\text{[math]}$ ，则 $\text{[math]}$ °， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是；

(2) 迁移探究：如图2，（1）中的其他条件不变，当 $\text{[math]}$ 绕点O逆时针旋转，点D正好落在 $\text{[math]}$ 的角平分线上，得到 $\text{[math]}$ ，求出此时 $\text{[math]}$ 的度数及 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系；

(3) 拓展应用：如图3，在等腰三角形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .将 $\text{[math]}$ 绕点O旋转，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， F是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ .当 $\text{[math]}$ 时，请直接写出 $\text{[math]}$ 的长.

综合题普通

3. 在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．

(1) 如图1，若点F与点A重合，求证：AC=BC；

(2) 若∠DAF=∠DBA，

①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；

②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．

综合题普通