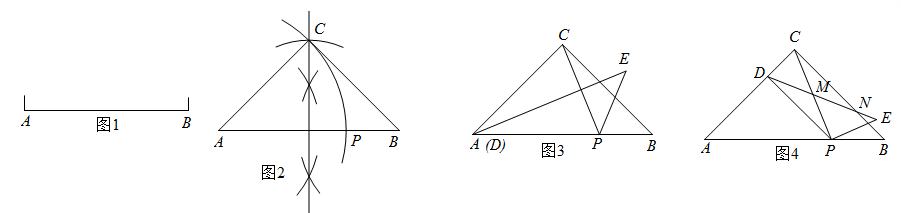
小东在做九上课本123页习题：“1：也是一个很有趣的比．已知线段AB（如图1），用直尺和圆规作AB上的一点P，使AP：AB＝1：．”小东的作法是：如图2，以AB为斜边作等腰直角三角形ABC，再以点A为圆心，AC长为半径作弧，交线段AB于点P，点P即为所求作的点．小东称点P为线段AB的“趣点”．

0 返回出卷网首页

1. 小东在做九上课本123页习题：“1： $\text{[math]}$ 也是一个很有趣的比．已知线段AB（如图1），用直尺和圆规作AB上的一点P，使AP：AB＝1： $\text{[math]}$ ．”小东的作法是：如图2，以AB为斜边作等腰直角三角形ABC，再以点A为圆心，AC长为半径作弧，交线段AB于点P，点P即为所求作的点．小东称点P为线段AB的“趣点”．

(1) 你赞同他的作法吗？请说明理由．

(2) 小东在此基础上进行了如下操作和探究：连结CP，点D为线段AC上的动点，点E在AB的上方，构造△DPE，使得△DPE∽△CPB．

①如图3，当点D运动到点A时，求∠CPE的度数．

②如图4，DE分别交CP，CB于点M，N，当点D为线段AC的“趣点”时（CD＜AD），猜想：点N是否为线段ME的“趣点”？并说明理由．

【考点】

余角、补角及其性质; 平行线的性质; 相似三角形的判定与性质; 解直角三角形; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在Rt△ABC中，∠ACB=90°，点D为AB上一点.

(1) 如图1，若CD⊥AB，求证：AC²=AD·AB；

(2) 如图2，若AC=BC，EF⊥CD交CD于H，交AC于F，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值；

(3) 如图3，若AC=BC，点H在CD上，∠AHD=45°，CH=3DH，则tan∠ACH的值为.

综合题普通

2. 我们经常会采用不同方法对某物体进行测量，请测量下列灯杆AB的长．

(1) 如图1所示，将一个测角仪放置在距离灯杆AB底部a米的点D处，测角仪高为b米，从C点测得A点的仰角为α，求灯杆AB的高度．（用含a，b，ａ的代数式表示）

(2) 我国古代数学家赵爽利用影子对物体进行测量的方法，在至今仍有借鉴意义图2所示，现将一高度为2米的木杆CG放在灯杆AB前，测得其影长CH为1米，再将木杆沿着BC方向移动1.8米至DE的位置，此时测得其影长DF为3米，求灯杆AB的高度

综合题困难

3. 如图，在矩形ABCD中，AB=6，BC=8，点E是BC的中点，点P为对角线BD上的动点，设BP=t(t>0)，作PH⊥BC于点H，连结EP并延长至点F，使得PF=PE，作点F关于BD的对称点G，FG交BD于点Q，连结GH，GE。

(1) 求证：EG∥PQ；

(2) 当点P运动到对角线BD的中点时，求△EFG的周长；

(3) 在点P的运动过程中，△GEH是否可以为等腰三角形？若可以，求出t的值；若不可以，说明理由。

综合题普通