1.
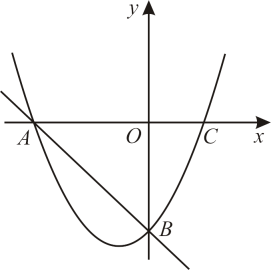
抛物线 交
交 轴于
轴于 ,
,  两点(
两点( 在
在 的左边),
的左边), 是第一象限抛物线上一点,直线
是第一象限抛物线上一点,直线 交
交 轴于点
轴于点 .
.
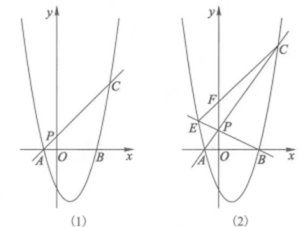
(1)
直接写出 ,
,  两点的坐标;
(2)
如图(1),当
两点的坐标;
(2)
如图(1),当 时,在抛物线上存在点
时,在抛物线上存在点 (异于点
(异于点 ),使
),使 ,
,  两点到
两点到 的距离相等,求出所有满足条件的点
的距离相等,求出所有满足条件的点 的横坐标;
(3)
如图(2),直线
的横坐标;
(3)
如图(2),直线 交抛物线于另一点
交抛物线于另一点 , 连接
, 连接 交
交 轴于点
轴于点 , 点
, 点 的横坐标为
的横坐标为 .求
.求 的值(用含
的值(用含 的式子表示).
的式子表示).
【考点】
一元二次方程的根与系数的关系(韦达定理);
两一次函数图象相交或平行问题;
二次函数图象与坐标轴的交点问题;
二次函数与一次函数的综合应用;
能力提升