1.
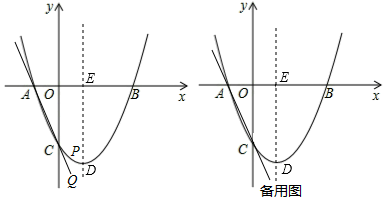
如图,抛物线 与
与 轴交于
轴交于 、
、 两点,与
两点,与 轴交于点
轴交于点 , 其顶点为点
, 其顶点为点 , 连结
, 连结 .
.
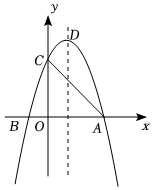
(1)
求这条抛物线所对应的二次函数的表达式及顶点 的坐标;
(2)
在抛物线的对称轴上取一点
的坐标;
(2)
在抛物线的对称轴上取一点 , 点
, 点 为抛物线上一动点,使得以点
为抛物线上一动点,使得以点 、
、 、
、 、
、 为顶点、
为顶点、 为边的四边形为平行四边形,求点
为边的四边形为平行四边形,求点 的坐标;
(3)
在(2)的条件下,将点
的坐标;
(3)
在(2)的条件下,将点 向下平移5个单位得到点
向下平移5个单位得到点 , 点
, 点 为抛物线的对称轴上一动点,求
为抛物线的对称轴上一动点,求 的最小值.
的最小值.
【考点】
待定系数法求二次函数解析式;
平行四边形的性质;
解直角三角形;
二次函数图象上点的坐标特征;
三角形全等的判定-AAS;
能力提升