1.
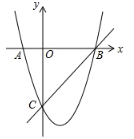
如图,已知抛物线:  与x轴交于点A,
与x轴交于点A,  (A在B的左侧),与y轴交于点C,对称轴是直线
(A在B的左侧),与y轴交于点C,对称轴是直线  ,P是第一象限内抛物线上的任一点.
,P是第一象限内抛物线上的任一点.
(1)
求抛物线的解析式;
(2)
若点D为线段  的中点,则
的中点,则  能否是等边三角形?请说明理由;
(3)
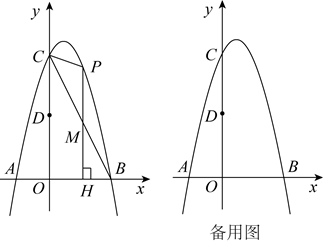
过点P作x轴的垂线与线段
能否是等边三角形?请说明理由;
(3)
过点P作x轴的垂线与线段  交于点M,垂足为点H,若以P,M,C为顶点的三角形与
交于点M,垂足为点H,若以P,M,C为顶点的三角形与  相似,求点P的坐标.
相似,求点P的坐标.
【考点】
待定系数法求二次函数解析式;
等边三角形的性质;
相似三角形的性质;
锐角三角函数的定义;
点的坐标与象限的关系;