1.
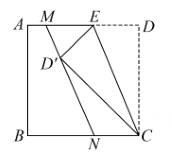
如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为.


【考点】
菱形的判定与性质;
正方形的性质;
轴对称的应用-最短距离问题;
翻折变换(折叠问题);
相似三角形的判定与性质;