1.
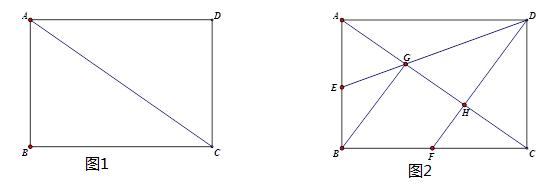
如图1,在矩形ABCD中,  ,
,  .点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作
.点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作  ,交AB于点F.
,交AB于点F.

(1)
求证:  ;
(2)
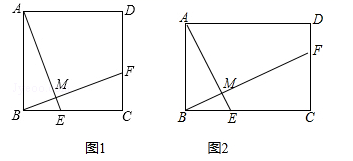
如图2,连接CF,过点B作
;
(2)
如图2,连接CF,过点B作  ,垂足为G,连接AG.点M是线段BC的中点,连接GM.
,垂足为G,连接AG.点M是线段BC的中点,连接GM.
①求 的最小值;
②当 取最小值时,求线段DE的长.
【考点】
两点之间线段最短;
矩形的性质;
点与圆的位置关系;
相似三角形的判定与性质;
直角三角形斜边上的中线;
能力提升