如图，在菱形ABCD中，∠BAD = 120°，AB = 6，连接BD ．

0 返回出卷网首页

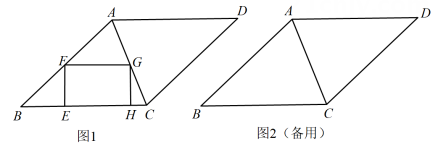
1. 如图，在菱形ABCD中，∠BAD = 120°，AB = 6，连接BD ．

(1) 求BD的长；

(2) 点E为线段BD上一动点（不与点B，D重合），点F在边AD上，且BE= $\text{[math]}$ DF，

①当CE丄AB时，求四边形ABEF的面积；

②当四边形ABEF的面积取得最小值时，CE+ $\text{[math]}$ CF的值是否也最小？如果是，求CE+ $\text{[math]}$ CF的最小值；如果不是，请说明理由．

【考点】

菱形的性质; 四边形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在菱形ABCD中，对角线AC与BD相交于点O，AB=8，∠BAD=60°，点E从点A出发，沿AB以每秒2个单位长度的速度向终点B运动，当点E不与点A重合时，过点E作EF⊥AD于点F，作EG∥AD交AC于点G，过点G作GH⊥AD交AD（或AD的延长线）于点H，得到矩形EFHG，设点E运动的时间为t秒

(1) 求线段EF的长（用含t的代数式表示）；

(2) 求点H与点D重合时t的值；

(3) 设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位，求S与t之间的函数关系式；

(4) 矩形EFHG的对角线EH与FG相交于点O′，当OO′∥AD时，t的值为；当OO′⊥AD时，t的值为．

综合题困难

2. 如图所示，已知四边形ABCD，ADEF都是菱形，∠BAD=∠FAD，∠BAD为锐角．

(1) 求证：AD⊥BF；

(2) 若BF=BC，求∠ADC的度数．

综合题困难

(1) 如图①，点A，点B在线段l的同侧，请你在直线l上找一点P，使得AP+BP的值最小（不需要说明理由）．

(2) 如图②，菱形ABCD的边长为6，对角线AC=6 $\text{[math]}$ ，点E，F在AC上，且EF=2，求DE+BF的最小值．

(3) 如图③，四边形ABCD中，AB=AD=6，∠BAD=60°，∠BCD=120°，四边形ABCD的周长是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．

综合题困难