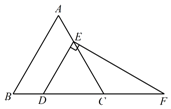
如图，已知等边的边长为4，点D、E分别是、的中点，过点D作，交的延长线于点F，求的长．

0 返回出卷网首页

1. 如图，已知等边 $\text{[math]}$ 的边长为4，点D、E分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，过点D作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点F，求 $\text{[math]}$ 的长．

【考点】

等边三角形的性质; 含30°角的直角三角形; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. $\text{[math]}$ 是边长为 $\text{[math]}$ 的等边三角形，动点P、Q同时从A、B两点出发，分别沿 $\text{[math]}$ 、 $\text{[math]}$ 方向匀速移动，它们的速度都是 $\text{[math]}$ ，当P到达点B时，P、Q两点停止运动，设P点运动时间为t（ $\text{[math]}$ ），当t为值时， $\text{[math]}$ 为 $\text{[math]}$ ？

解答题容易

2. 如图，等边 $\text{[math]}$ 的顶点分别在等边 $\text{[math]}$ 的各边上，且 $\text{[math]}$ 于点E．若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

填空题容易

3. 等边三角形的边长为2，则它的周长为．

填空题容易