1.
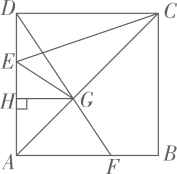
如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.

(1)
求证: .
(2)
若
.
(2)
若 .
(3)
若
.
(3)
若 , 当
, 当 的大小发生变化时(
的大小发生变化时( ),在AE上找一点T,使GT为定值,说明理由并求出ET的值.
),在AE上找一点T,使GT为定值,说明理由并求出ET的值.
①求菱形的面积.
②求的值.
【考点】
两条直线被一组平行线所截,所得的对应线段成比例;
相似三角形的判定与性质;
解直角三角形;
四边形的综合;
能力提升